预测准确度有三种常见的计算方式:绝对误差、绝对百分比误差、均方误差。下面我们通过一个例子来说明。
如表1,第4周的预测是77,实际需求是89,那么误差就是77-89 = -12,绝对误差= |-12|=12,绝对百分比误差= |-12| ÷ 89 = 13%,均方误差=
要说明的是,说是准确度,这里计算的其实是误差。有的误差能转换成准确度,比如1-绝对百分比误差,就得到准确度;有的则没法简单转换,比如绝对误差和均方误差。但不管怎样,误差越小,意味着准确度也越高。
表1:预测误差的计算示例
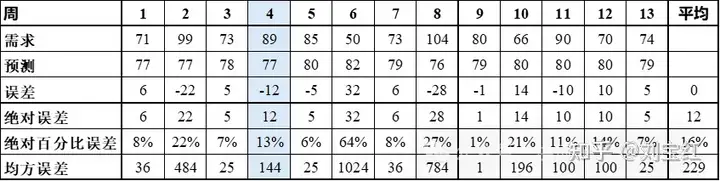
从其计算方式可以看出,这三种预测准确度指标各有优劣。
平均绝对误差的好处是直观,容易理解,易于跨职能沟通。如果损失跟偏差成正比的话(比如单价是10元,那么少预测1个,营收就损失10元;少预测2个,营收就损失20元),基于平均绝对误差来选择合适的预测模型,也挺有道理。
但实际上,误差跟损失往往不成正比,特别对于极端误差来说。
就拿预测低估来说,少预测1个,我们可以很容易地用安全库存来应对,运营成本为零,也不会损失营收;但少预测100个的话,就可能得赶工加急,产生很多运营成本,而且可能丧失营收、失去客户,成本远非少预测1个的100倍。预测高估也是同理:多预测1个,没问题,下一期用掉就行;多预测100个,则可能得折价甚至报废处理,单位成本显然更高。
均方误差通过对误差平方,来放大极端误差,加倍"惩罚"那些极端误差。要知道,小的误差没关系,我们可以通过安全库存、供应链执行来轻松应对;害死我们的是大错特错,也就是那些极端误差----预测过于低的话,安全库存很容易被击穿,导致高昂的赶工加急成本;预测过于高的话,则容易造成大量的积压,以及由此而来的呆滞库存。
如图1,6月、10月的绝对误差最大,我们通过平方,加倍"惩罚"这样的极端误差,最终反映在较高的12个月均方误差中。选择预测方法时,要尽量避免产生大错特错、极端误差的预测模型。用均方误差来量化预测准确度,能较好地排除这样的模型,也符合业务逻辑。
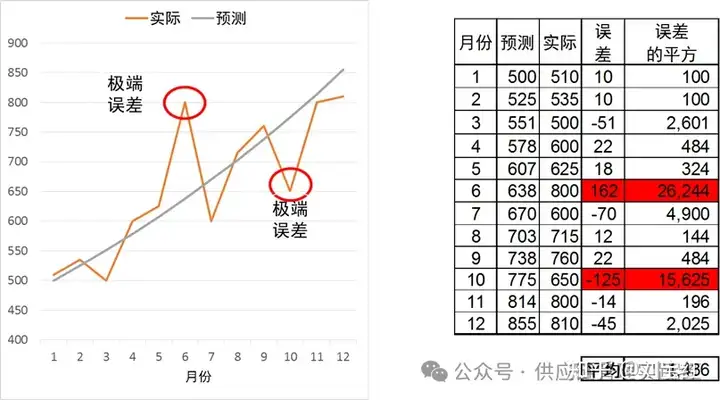
图1:均方误差示意
均方误差的一个问题是不够直观。比如在图1中,均方误差4436究竟意味着什么,谁也说不清。不过"不怕不识货,就怕货比货",在比较多种方法时,均方误差越小,表明预测模型越准确,这就足够了。还有,均方误差对极端值很敏感,可能导致过高估计误差。这也展示了预测模型择优时,清洗极端值的重要性。
让我们再回到平均绝对误差。
平均绝对误差跟需求的大小有关。比如平均需求是1000,平均绝对误差是100的话,这预测是相当准确;但如果平均需求是10,平均绝对误差还是100的话,这预测就相当糟糕了。所以,需求量显著不同的产品,在平均绝对误差上是没有可比性的,不能基于这一指标来评判哪个产品的预测更准确。均方误差也有同样问题。
解决方案呢,就是用绝对百分比误差,本书有时简称为百分比误差。这其实相当于对误差进行归一化处理,让不同产品之间的预测准确度有了可比性。百分比误差的好处还有直观,跨职能沟通容易,因而被很多企业采用,或许是这一指标的应用最广的原因。
绝对百分比误差的缺点是分母太小或为零时,百分比就很高甚至没法计算,导致严重失真。对于长尾慢动产品,这个问题就更大了。我们的常见应对方案有二:要么设立上限,比如误差最大不能超过100%;要么采用均方误差、绝对误差。
百分比误差也会有误导:需求是10个,预测了6个,准确度是60%;需求是60个,预测了36个,准确度也是60%。但是,他们对业务的影响不同。第一种情况下,损失了4个的生意,第二种情况下,24个。跟绝对误差、均方误差结合使用,可适当弥补这一问题。
到现在为止,我们介绍了常用的三种预测准确度(更严格地讲,预测误差)的统计方式。还有些别的统计方式,我们这里不再赘述。那究竟该用哪种准确度指标呢?没有一刀切的答案。企业里常见的是百分比误差,但学术文章中更常见的是均方误差、均方根误差,尤其在机器学习、人工智能领域。
计划软件一般能输出多个准确度指标。要注意的是用不同指标,预测模型择优的结论可能不同。比如用百分比误差,可能模型A更准确;但用均方误差时,模型B可能更准确。





评论