季节性强，一锤子买卖如何预测？

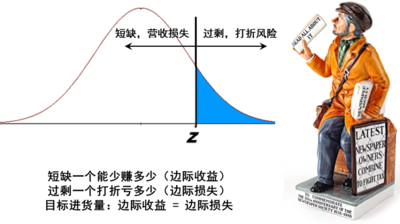
这种产品的典型就是日报：作为报童，每天进多少张报纸最合适？进得多了卖不掉，最后打折直至扔掉，是库存成本；进得少了不够卖，有营收损失，是机会成本。学者们研究了多年的"报童模型"，如图 1，就是从数理统计的角度来模拟这两种成本。直观地讲，进货的数量越小，卖掉最后一张报纸的概率越大，这时候边际收益高于边际成本；进货的数量越大，卖掉最后一张报纸的概率越低，边际成本渐渐超过边际收益；当两者的边际期望值相等的时候，就是最佳的进货量。

图 1："报童模型" 权衡收益与损失，设定合理的进货量

"报童模型"的应用范围非常广，特别是产品的生命周期很短的环境，比如生鲜，面包，糕点等。"不卖隔夜肉"的钱大妈就是典型的例子：凡是当天进店的货，当天就得卖完；到了晚上7点就开始打折，半小时打一折，一直到免费派送（如图 2）。我在深圳的培训场地旁边，就有钱大妈的一个门店，我经常在晚上8点左右过去看看，那时货已经清得差不多了。这后面的逻辑就是"报童模型"：假定这个门店要进20斤胡萝卜，有多少斤能全价卖掉，多少打九折，多少打八折，这根据过去本店、同类店的销售历史能够量化，求出相应的概率，匹配上相应的成本和收益，就构成"报童模型"的输入参数，反推过来求得最佳的进货量。

图 2：钱大妈的清货时间表

或许有人会说，有销售历史的好办，但问题是在快消品行业，产品当季上当季下，没有需求历史怎么办？我们可以考虑专家判断法，组织来自销售、产品、计划、运营等多个职能的专家，根据以前有可比性的产品，分别背靠背独立预测这个产品的销量（背靠背是为了减小相互影响，特别是强势人物、强势职能的影响）。围绕多个预测值，我们可以求其平均值、标准差，得到图 1中那样的正态分布曲线。然后我们量化边际收益与边际损失，确定最终的预测。

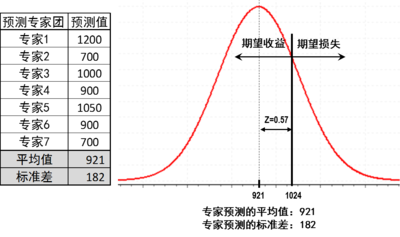
比如上面案例中的快时尚产品，专家团队有7个，每个人的预测见图 3，专家团队的预测平均值是921件，标准差是182（假定需求服从正态分布）。假定卖掉一件，毛利是50元；卖不掉的话，每件的损失是20元。假定缺货率是x，那么边际缺货带来的毛利损失就是50*x；相应地，边际过剩带来的成本损失就是20*（1-x），边际收益等于边际损失的方程如下：

50*x=20*(1-x)

x = 29%

也就是说，该产品的最佳有货率是（1-29%）=71%，相对应的Z值是0.57，乘以标准差182，等于103件。这就是说，如果我们备921+103=1024件的话，我们的边际收益就等于边际损失，实现利润的最大化，这就是对该产品的最佳进货量预测，如图 3。

图 3：一锤子买卖的最佳进货量

对于这种一锤子买卖式的预测，由于供应周期很长（比如案例产品的整个周期在3个月左右），需求的不确定性很高，我们还可以设置多个推拉结合点，采取逐点推拉的供应链执行，进一步管控库存风险。

比如有个快时尚企业采取442的做法：把40%的做成成品，40%做成半成品，20%留作原材料（当然，这比例可以根据产品的具体情况调整）。对于已经做成成品的40%，又进一步分解，其中20%的铺货，推到销售渠道、门店；另外20%留在总库，用于补货。这样，从原材料到半成品到成品，再到渠道，该企业建立了多个推拉结合点，根据成品的销售情况，定期更新需求预测，动态平衡短缺与过剩风险，决定把多少原材料加工成半成品，多少半成品加工成成品。