时间序列的预测：指数平滑法

指数平滑法在上世纪50年代发展成熟，在实践中应用很广。百度百科上甚至说，"所有预测方法中，指数平滑是用得最多的一种"[1]。就我个人的经验而言，在北美、欧洲的供应链领域，指数平滑已经是很常用[2]----跟来自这些地区的外资企业提起，熟悉指数平滑法的人挺多；但跟本土企业提起，熟悉的人就相对少多了。

对于时间序列的三种情况（随机，趋势，季节性），指数平滑法都有相应的方法来预测：简单指数平滑法应对相对平稳的情况，霍尔特双参数法应对趋势，霍尔特--温特模型应对季节性加趋势。在阐述中，简单指数平滑法往往也叫指数平滑法，我们这里谈的就是简单指数平滑法。

与移动平均法一样，简单指数平滑法用来预测下一步，把下一步的预测当做未来各期的预测，因此最适用于没有明显的趋势、周期性的平缓情形。让我们用X代表实际需求，F代表预测。那么，X_t就是第t期的实际需求，F_t+1就是下一期的预测，其中一部分来自上期实际值，剩余部分来自上期预测值，也就是说，是上期实际值与预测值的加权平均（公式1）。用另一种形式表述，就是下期的预测是在上期预测的基础上，根据误差做出一定的调整（公式2）。两种表述，区别只是形式上的，而实质内容是一样的。

F_t+1=αX_t + (1-α) F_t （公式1）

F_t+1= F_t+ α (X_t - F_t) （公式2）

0 ≤ α ≤ 1

通过调整平滑系数α，就可以调整上期实际与预测值的权重：α越大，上期实际值的权重越大，上期预测值的权重越小，预测模型表现地越灵敏，越能尽快反映实际变化，当然也越受随机因素影响，带给供应链的波动也越大；α越小，上期实际值的权重越小，上期预测值的权重越大，越多的变动被当做"杂音"过滤掉，预测也表现得越平稳，给供应链的运营成本越低，但风险是没法及时响应市场的需求变化。

经常有人问，这指数平滑法听上去很玄妙，其中的"指数"是怎么来的？"平滑"又是如何平滑的？让我们把上面公式1中的基本公式展开来阐述。我知道，你不喜欢这些公式，我也不喜欢。但是，为了表明我们比别人知道地多，有时候还不得不做一些简单的推导----请相信，这是本书唯一的一点公式推导，你也不用记住详细的公式。

如图 1，让我们把公式1层层展开，你会发现，需求历史是按照（1-α）的等比级数综合到预测中。比如第t期的权重是α（1-α）⁰，t-1期的是α（1-α）¹，t-2期的是α（1-α）²，依次类推。因为1-α的值介于0和1之间，所以次数越高，需求历史的权重就越小，以几何数级衰减，这就是指数平滑法中"指数"的来历。

从图 1也能看出，指数平滑系数α越大，需求历史的权重衰减地越快，也意味着最新需求历史的权重越大，预测模型也就越响应。相反，α越小，需求历史的权重相对衰减越慢，最新需求历史所占权重也相对越小，预测模型也就越稳定。

这也让指数平滑法比移动平均法更加灵活：（1）通过选择不同的平滑系数，指数平滑法可以更好地匹配业务的变化；（2）加权式平滑，需求历史越近，权重越大，让指数平滑法能更快地响应需求变化。

在当今影响需求的方法越来越多，需求变动越发频繁的情况下，指数平滑法的这些优点能给我们很多帮助，让我们能够尽快快速响应。比如门店或渠道在做促销，前置库位的需求突然增加；新产品导入，带动关联产品的需求；气温升高，带动相应产品的需求，都可以通过指数平滑法尽快发现，及时驱动总仓补货。

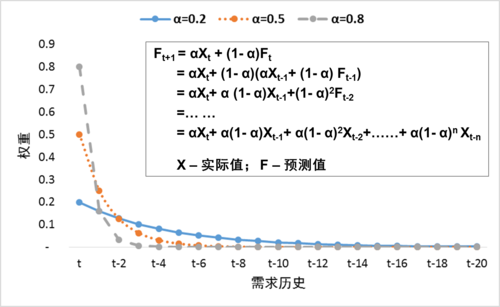
图 1：指数平滑法中，需求历史的权重按照指数级别衰减

简单指数平滑法其实是移动平均法的一种，是加权移动平均，而且权重以几何级数递减。指数平滑法有一系列的优点，这里主要总结为三个方面：简单，响应，可以持续优化。

先说简单。对移动平均法来说，移动几期平均，就得保留多少期的需求历史；但对简单指数平滑法来说，我们只需要保留两个数值：上次实际值、上次预测值。这在计算机应用尚不广泛，人类的计算能力尚有限的时候，尤其重要。有时候，你不得不佩服，这些半个多世纪前的研究者们，能够找出这么简单而美妙的方法来，真正的数学美。

再说响应。简单指数平滑法是一种加权移动平均法，需求历史越新，其权重越大（参见图 8），这意味着对于新近发生的，模型可以很快捡起，反映到下一步的预测中，在快速纠偏上做得更好。这对于延续性强的业务环境很有帮助。比如促销、活动不断，很多时候前端在促销，后端根本不知道，但简单指数平滑模型已经从昨天的销量探知了，驱动明天多补货。对于爆款，简单指数平滑法一般比移动平均法的预测效果会更好。

在备品备件领域，特别是高值慢动的产品，需求很不频繁，但一旦发生，往往意味着很多（小概率事件不容易发生，一旦发生则意味着不再是小概率事件）：是不是这批设备用到一定年限了，需要更换相应的备件，或者产线在做什么预防性维修等。简单指数平滑法能够更好地迅速捡起这一信号，尽快调整预测，驱动供应链尽快响应。我以前在备件计划领域，用的软件是由沃顿商学院的教授和博士们开发，其中预测模块用的就是简单指数平滑法。

最后说持续优化。移动平均法的优化比较复杂，要么得用不同期数的需求历史，要么得用加权平均；简单指数平滑法就简单多了，只要调整平滑系数一个参数即可。我们可以手动代入不同的值，也可以在Excel中用Solver来帮助平滑系数的择优。

鉴于这些优点，我鼓励大家在移动平均法外，多尝试简单指数平滑法，特别是在B2C行业，改变需求的行为比较多，需求的关联性比较高的情况下。有些B2B情况也类似。比如产线上的某个关键备件坏了，可能意味着其他设备上的该零件都接近生命周期末期，我们当然希望预测模型给这个最近发生的需求更多权重，而不是跟过去两年的需求简单平均掉----指数平滑法是绝好的选择。

当然，优点这么多，简单指数平滑法的挑战也不少。

其一是简单指数平滑法虽然只有一个系数，但该平滑系数的优化不易。相比移动平均法，指数平滑法更加"精致"，而这所有的"精致"，都是通过微调平滑系数这一个参数来实现，而且以抽象的指数方式衰减（而不是我们容易理解的线性方式）。就如越是精密的仪器，参数调整就越重要一样，选择合适的平滑系数对指数平滑法至关重要而，我们在后面还会讲到。

其二是简单指数平滑法适合于短期预测，比如预测下一期的补货挺好，但要预测时段长了，虽然我们假定未来每期的需求都一样，都等于下一期的预测，但时间跨度越长，这个假定越难成立。

其三，跟移动平均法一样，简单指数平滑法是滞后的，一旦需求表现出趋势、季节性等，指数平滑法就一直处于"追赶"状态，我们得考虑更合适的指数平滑模型，比如霍尔特（趋势）和霍尔特-温特（季节性加趋势）模型。

此外，指数平滑法的名称听上去有点高大尚，高冷玄妙，容易吓退"追求者"。其实这只是心理障碍，一旦突破，就没有问题了----到现在为止，你已经读完了指数平滑法上技术含量最高的部分，相信已经发现，指数平滑法其实也没什难的，关键是要尝试用起来，边用边改进。