霍尔特法得名于查尔斯·霍尔特,最早发表于1957年,成为预测上用得最广的模型之一[1]。对需求预测和库存计划来说,上世纪50、60年代可以说是人才辈出。这里我想特别介绍一下美国的HMMS研究团队。这个团队的名称来自四位研究者姓氏的第一个字母(Holt,Modigliani,Muth和Simon),当时他们都在卡内基工学院[2],旨在是寻找更好的决策机制,以帮助工业界更好地应对种种库存、生产和计划问题。这些问题在宏观层面导致经济危机,在微观层面让企业经常处于危机状态,要么是赶工加急,要么是产能利用不足,以及库存积压。
Holt就是这里要讲的霍尔特,他开发了应对平缓需求的简单指数平滑法、应对趋势的霍尔特双参数线性指数平滑法,以及应对季节性的霍尔特--温特模型,这些都成为工业界最为广泛应用的预测模型[3]。其余的3位研究者中,Modigliani和Simon后来获得了诺贝尔经济学奖,而Muth的理性预期模型呢,又成为卢卡斯获取诺贝尔奖的基石。不得不感叹,这真是个才华横溢的研究团队啊,那时的卡内基梅隆就已经是个才俊辈出的地方。
简单地说,霍尔特法就是在简单指数平滑系数α的基础上,增加了一个趋势的平滑系数β,所以也叫"双参数平滑法"。当β等于0的时候,霍尔特模型就成了简单指数平滑法。
当需求呈现明显的趋势,比如图 1中的情况,简单指数平滑法没法有效应对,表现在对平滑系数择优时,你会发现最优的α变成了1,或者非常接近1----简单指数平滑法没法有效预测时,就只能"步步紧逼","球"跑到哪里,就跟到哪里,这注定被动反应,永远滞后一步。霍尔特法增加了趋势参数,更好地预判"球"的走向,系统地增加了拦截到"球"的胜算。
在霍尔特双参数平滑法模型中,预测由两部分构成;一部分是水平部分,是在上期水平部分的基础上,用简单指数平滑法来更新;另一部分是趋势部分,是在上期趋势部分的基础上平滑调整,也用简单指数平滑法来更新;两者相加,就得到下期的预测[4]。
霍尔特法不但持续调整水平部分,而且持续调整趋势部分,在横向和纵向两维调整预测,所以能更好地应对趋势的变化。基本的公式分三部分,更多细节可以百度"霍尔特双参数指数平滑法"。
本期水平部分=α*本期需求实际值 + (1-α)*(上期水平部分+上期趋势部分)(1)
本期趋势部分=β*(本期水平部分-上期水平部分)+(1-β)*上期趋势(2)
下期预测=本期水平部分 + 本期趋势部分(3)
因为有趋势,霍尔特法可以预测多期的值:未来第n期的预测等于本期水平部分加上n倍的趋势部分。比如在图 1的例子中,第22周的预测=40+1*(-18)=22,第23周的预测=40+2*(-18)=4。你马上会发现,第24周的预测就成了负数,这显然不合理----这是趋势参数带来的问题,导致霍尔特法有过度预测的倾向,在使用的时候要加以留意。
霍尔特双参数平滑法中,平滑系数α和β介于0和1之间。与简单指数平滑法一样,这两个平滑系数越大,预测模型就越响应,也就是说最新发生的对下一步的预测影响更大,风险是有可能过度反应;平滑系数越小,预测模型就越平稳,也就把最新发生的更多地当成"杂音"给过滤掉,风险是可能没法及时响应需求变动。
在霍尔特参数的择优中,我们也可以用Excel中的Solver插件,基于预测准确度最高的目标,围绕两个参数α和β优化,选择最优的参数。
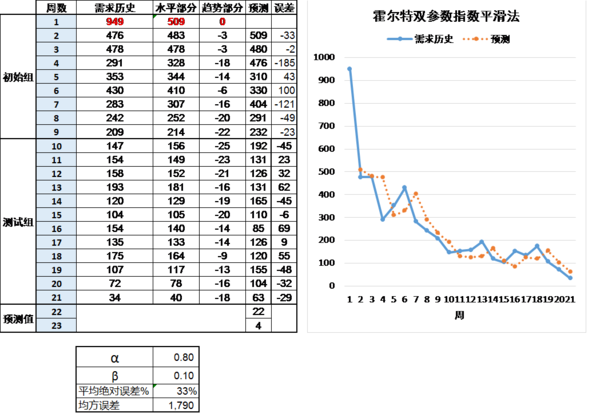
图 1:用霍尔特双参数指数平滑法来预测
与简单指数平滑类似,霍尔特双参数也需要初始化。
在初始化时,可以假定初始"水平部分"为第一个实际需求值,初始"趋势部分"为第二个实际需求值减去第一个实际需求值;也可以基于前几个实际需求值,利用线性回归模型来计算截距(水平部分)和斜率(趋势部分)。当然还有别的方法来初始化,比如把趋势部分的初始值设为0[5](这是假定刚开始的时候没有趋势),以及用前几期的平均值作为水平部分的初始值。
跟前面简单指数平滑法的情况类似,经过一段时间的初始化后,模型会自动纠偏,初始值的影响变得有限,直至微乎其微。
在图 1的例子中,我们用前9期的数据来初始化,用后12期的数据来测试模型、选择最优的模型。鉴于前几个数据相当离散,我们用前5期的平均值作为水平部分的初始值,趋势部分的初始值设为0,α取值0.8,β取值0.1。对于测试组而言,预测的平均绝对误差为33%,均方差为1790。我也尝试用简单指数平滑来预测,最优化的平滑系数接近1,这两个准确度指标分别为37%和1869。显然,对于这个快消品来说,需求变化剧烈,一经导入就达到顶峰,需求然后就一路下滑,与简单指数平滑法相比,霍尔特法是更有效的预测方法。
当然,对于指数平滑法,到现在为止,你读了可能没有什么感觉。这没关系,先了解一下,然后动手实践,在实践中加深理解。毕竟,不管理论多完美,除非下到水里,是没法学会游泳的。
【实践者问】我的专业是工业工程,目前感兴趣的工作有两方面,一个是计划,另一个跟供应链稍微偏差些,是数据分析。我由于本身专业跟供应链很相关,而且对于生产计划这样与数据打交道的工作也很感兴趣,但是专业课上学到的无外乎移动平均法、指数平滑法、霍尔特法这些,感觉一个外行人用点心,一天就能熟练掌握几种预测方法,我想知道在计划这个行业进一步是什么样的职业发展道路?
【刘宝红答】这些基本的方法能够解决需求计划的大部分问题,所以不要小看它们。它们看上去简单,其实不简单,不然的话为什么还要把人名冠上去?像霍尔特这种专家,都是跟诺贝尔奖获得者相提并论的人。这些方法凝聚着众多研究者多年的心血,远远没有想象的那么简单----如果我们认为简单,那八成是因为我们不理解。
比如移动平均法是简单,但是究竟用多少期的需求历史就很不简单,因为这要求我们懂得如何去评估预测模型的好坏。这又涉及到绝对误差、均方差等预测准确度的统计方法----均方差又让我们意识到,预测的一大关键是避免大错特错:小的预测失误容易对付,可以通过安全库存、供应链执行来解决;害死我们的是大错特错。
那大错特错又是怎么发生的?选择了不合适的预测模型,用了不合适的参数是一个原因,但基础数据也是一大问题源,比如数据没有清洗,我们把以前促销的数据包括在内,后续需求预测自然显著偏高。这是对发生了的促销,那没有发生的呢?这又涉及到跟销售端的对接----需求预测是"从数据开始,由判断结束",数据代表已经发生的,可重复的;判断代表还没有发生的,不可重复的,这又牵扯到销售跟运营协调流程,企业的几大主干流程之一。
所以,不要低估这些基本的模型。运用得当,这些模型能解决大部分的问题。不要求新求异。如果有人跟你大谈卡尔曼滤波,或者灰色预测法什么的专业名词,你应该敬而远之----我不是说这些不重要,而是说那更多的是龙肝凤胆;我们得回归计划的基本面,先把我们的大米饭做得更好更合口再说。
这就如练武,不管你学什么武术,基本的招数也就那些。要经过一遍又一遍的练习,熟能生巧,出神入化的时候,才能真正掌握。要知道,高手的高,并不在于他们知道的招数比别人多,而是在相同的招数里,他们得到更多。
[1] 这篇经典文章的名称是Forecasting seasonals and trends by exponentially weighted moving averages, Charles Holt, ONR Research Memorandum No 52, Carnegie Institute of Technology, 1957。这份研究是由美国海军资助的。在美国,运筹学、运营管理的很多早期研究是由军方资助的,为以后的供应链管理学科打下坚实的理论基础。
[2] 该学院由钢铁巨头卡内基创建,后来与梅隆学院合并,成为今天蜚声海外的卡内基梅隆大学。
[3] Learning How to Plan Production, Inventories, And Work Force, Operations Research, Vol. 50, No. 1, January-February 2002, Charles c. Holt, pp. 96-99.
[4] 我在查阅中文文献,对类似的专业术语,很难找到合适的翻译:那些文献要么用公式中的字母代替,这多出现在学者的文章中;要么就采用英语原名,这多出现在外资背景的职业人写的文章中。这些本来很简单的方法论,却被很多著述弄得异常晦涩难懂----一旦开始卖弄"数学之美",推导出一串又一串的公式时,这些很实用的方法论就成了学究们的自娱自乐,对我们实践者来说无异于灾难。当本土企业开始大面积用这些的时候,很通俗、很贴切的中文名称就会出现----现在还没到那一步。
[5] 比如在Real-Statisitics.com网站,Charles Zaiontz博士的霍尔特法Excel中,趋势部分的初始值就用0。这位博士开发了各种各样的Excel表格,用来解决数理统计的问题,包括简单指数平滑法和霍尔特法,是学习这些预测模型的很好资料(http://www.real-statistics.com/time-series-analysis)。 他以前在美国的大学任教,现居住在意大利。像他那样把复杂的数理统计解释得那么清楚,这世界上可没有多少人。我以前读MBA时,教统计学的那位教授就是这样的人。他让我真正体会到统计学反映出的简单美(惭愧,快20年过去了,我连他的名字都忘了)。这也正是人工智能等没法广泛应用的原因之一:我跟好几个人工智能公司的专家谈,他们都在尝试用人工智能来解决需求预测问题,但没有一个人能够解释清楚,人工智能究竟是怎么运作的,能更好地预测需求----我在计划领域可以说是高于平均水平,他们在人工智能上是远超平均水平,我们在一起都没法搞清楚人工智能是怎么回事,一般的计划经理、计划员怎么能搞清楚呢?不理解就不信任,不信任就不会去用。





评论