有一次,我在旧金山参加高科技预测与计划峰会。一个赞助商在展台上放一大瓶巧克力豆,让每一个与会人员有奖竞猜。挺大的一个瓶子,几百只巧克力豆,谁又能猜得准呢?几十个与会者猜下来,有猜1000只的,有猜200只的,有猜几十只的。但是,令人吃惊的是,平均值竟然只与实际值相差4只,误差在1%左右(实际值是296,平均值为292)。
这个游戏有多种版本,我在美国的好几个活动都见到过,里面放的东西可能不同,数量不同,参与者也不同,但结果都一样:大家看上去都是在瞎猜,但平均值都惊人地接近真相。
后来,我在国内几次重复这个实验,不过把巧克力改为糖。2019年8月30日,我在上海培训,有101位职业经理人参与竞猜。我让他们看着装糖的瓶子,扫描二维码填入各自猜的值。我还让一位学员现场清点,确认瓶子里实际装了多少颗糖,以示我没有作假。
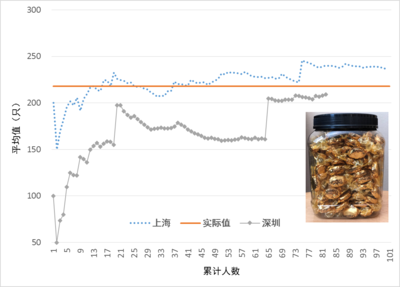
如图 1,我按照学员填写答案的先后次序,求累计答案的平均值。比如横轴是5,纵轴是196,意味着前5个人的平均答案是196,与实际值218的误差是-10%;横轴是30,意味着前30个人的平均值为211,与实际值218的误差是-3%。看得出,刚开始时,人数比较少,平均值的误差比较大;5个人以后,平均值的误差已经控制到10%以内,然后随着人数的增加,误差进一步降低,最后101个人的平均值准确度为92%。
图 1:瓶子里有多少颗糖
一周后,我在深圳培训中做同样的实验,参与的人数稍微少点,共82位职业经理人。为了便于和上海的对比,我把深圳的结果也汇总在图 1中。
刚开始的时候,不知为什么,深圳学员的估计都显著偏低,估计是课前先到的一批学员看着教材上的图片在猜----图片相对实物小多了,可能让大家少猜。即便这样,13个人的时候,大家的平均值已经有70%的准确率。可不要小看这个70%:你去统计你们的那些成熟产品,需求历史相当长,需求也相当稳定,看有多少的预测准确度能超过70%。
随着越来越多的人参与竞猜,平均值的准确度继续提升,在20人的时候达到最高点91%。然后不知什么原因,大家猜的数值又开始保守起来,平均值的准确度也一路下降,但仍旧维持在75%上下。直到第65个人,冥冥中填了个大数字,一下子把准确度提升到94%,最终一直维持在百分之九十几的水平。你不得不佩服概率世界的奇妙:样本多了,有的人猜得少,有的人就猜得多;很多人猜得少,那就来一个猜得很多的抵消。
在概率论上,这背后的原理叫"大数定律",即大量重复相同实验时,随机变量的算术平均值会向特定值收敛。放在这个竞猜的游戏中,有的人会高估,有的人会低估,两相抵消,平均值会更接近真相。这样的例子比比皆是。比如身高,上辈人个头儿矮点,下辈人一般会高点,否则的话,三代五代人后,路上走的岂不都是武大郎。村子里老子比较弱,经常受欺负的,儿子往往强,变成欺负别人的人----老子英雄儿好汉往往不靠谱,王侯将相宁有种乎却是真的。三代必出纨绔,都是大数定律在起作用。
智慧在民间。三个臭皮匠,胜过一个诸葛亮,算是"大数定律"的民间版本。要知道,很多问题尽管看上去摸不着头脑,但大家总是或多或少有些经验,知道某一方面的知识、细节。这些细节知识整合起来,准确度就很高。放在专家预测上,有的人高估,有的人低估,多人预测降低了偏差,往往比单个人的预测更准确。





非常有意思的案例,充分展示了个体差异与基于一定样本的统计趋势,希望未来我也有机会能在培训里试一试,谢谢老师。