安全库存的设置是个技术活，其实核心就这些

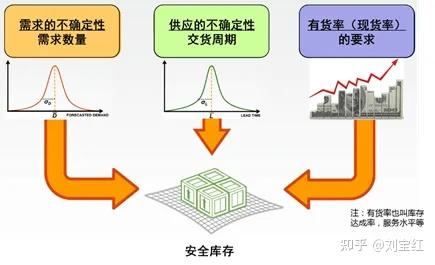
图1：安全库存的驱动因素

图片来源：http://elearning-examples.s3.amazonaws.com/Safety-Stock/player.html

对于安全库存，很多企业的做法是凭经验一刀切，设定一定天数的用量作为安全库存，比如A类物料放3周的量，B类物料放2周等。这些经验值凝聚着组织的很多智慧，简单易行，好沟通，不能一棍子打死；但是，一刀切注定有一刀切的问题。比如同样是A物料，但需求的不确定性不一样；或者同样的供应商，但不同的工艺下，供应的不确定性不一样；同类的产品，同样的供应商，同样的补货周期，但对有货率的要求不一样，这都会要求有不同的安全库存。一刀切的结果呢，注定是有的切多了，有的切少了，造成过剩的过剩，短缺的短缺，短缺与过剩并存，都是典型的计划问题。

那解决方案呢，就是量化需求的不确定性、量化供应的不确定性、量化有货率的要求，来计算安全库存。在实践中，供应的不确定性比较难以量化，比如有时候我们给供应商一个大订单，让分次送货；或者我们给供应商订单，又要求他们推迟交货等，都导致没法客观统计订单的交付周期。还有，如果跟供应商建立VMI、JIT的话，就根本没有订单，自然就没有简单、可靠的方法统计交付周期了。所以，我们往往假定供应周期是确定的，而在量化需求的不确定性、有货率的基础上，适当加以调整，比如多放几天的量，作为最终的安全库存[1]。

第一步：量化需求的不确定性

我们首先来量化需求的不确定性。简单地说，需求的不确定，就是我们能不能有效预测。当需求难以预测时，预测的准确度就低，实际需求与预测之间的误差就大，我们就得放越多的安全库存来应对。在数理统计上，我们用"标准差"来量化需求的不确定性[2]。

对于具体的产品，我们找到过去一段时间每期的预测和实际需求，计算两者之间的误差，围绕预测误差求其标准差，如图2，就能量化需求的不确定性。标准差越大，表明需求的不确定性越大，因而要放更多的安全库存来应对。这里有个基本假定，那就是需求历史的代表性，即过去和未来需求有一定的重复性。此外，我们也假定预测误差符合正态分布[3]。

从数理统计的角度看，为了让标准差的可靠性高，我们一般要求30个以上的数据点。但是，在实际操作中，我们往往没有那么多的数据点。我会尽量不要少于13个，这是一个季度的需求历史，按周统计。如果低于10个数据点的话，我会对统计结果非常谨慎----试想想，如果要画一个像样的正态分布曲线，你也至少得十几个点吧，从数理统计角度描述也是同样的道理。

图2：量化需求的不确定性

当需求相对稳定，需求历史本身符合正态分布的时候，我们可以直接围绕需求历史来求标准差，作为需求的变动性量化指标，如图3。这其实相当于把平均值当成预测，预测误差等于实际需求与平均值的差异，围绕差异求标准差。这种方式的好处是简单直观，容易理解，不用保留需求预测历史。

让我们实际演算一下来说明。如图3所示，第②列是过去20周的实际需求，第③列是过去20周需求历史的平均值，第④列是平均值与每周实际需求的差值（误差）。看得出，围绕第②和第④列求标准差，两者的结果完全相同。这就是说，我们可以求需求历史的标准差，用它来量化需求的变动性。

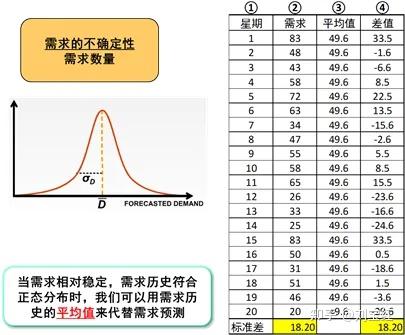
图3：需求相对稳定，符合正态分布时，需求的标准差就是其不确定性

正因为图3的情况简单，更容易计算标准差，所以被很多人滥用。比如有些需求有明显的趋势或者季节性，需求历史本身是不符合正态分布的，如果你预测的话，你也不会简单地用一段历史需求的平均值作为预测值。这时候，我们要回到图2中的方法。如果你以前已经在预测，那就计算每期预测与实际的偏差，围绕多期的偏差来求标准差；否则的话，你可以用以后要用的预测方法，复盘预测过去一段时间的需求，来计算误差及其标准差。

这里的假设是，特定的预测方法会有误差，而在历史上的误差与未来的误差整体上一致，也就是说，误差的历史有代表性，错的方式差不多。这就如员工A做事一直很仔细，差错很少，你以后也不会花很多时间检查她做的事；员工B有点马大哈，差错较多，你以前花了很多时间，以后也会花很多时间来检查他的工作----你都在假设两个员工的差错（误差）有延续性，过去的历史可以代表未来。

让我们看一个具体的例子。

如图4，这是很多人经常问我的：需求呈现明显的趋势或季节性，安全库存该怎么设置？这时候，你不能简单地摘取过去一段时间的需求历史，求其实际需求的标准差来量化需求的变动性----那样的话，需求的标准差会很大，比如在这个案例中是4704，导致我们高估而多放安全库存，造成更大的库存风险。

合适的做法是摘取一段需求历史，比如8到20周（13个数据点），找到每周的预测（如果没有的话，我们可以复盘，用以后要用的预测方法，来复盘这段时间每周的预测），计算每周的预测误差，围绕误差计算标准差，这个例子中是2163。然后，基于这个标准差计算安全库存（具体的计算稍后详介绍）。

要记住，因为需求变动，所以预测不准，安全库存的一大任务是应对预测的不准确，即预测的误差。所谓的需求变动性，是相对预测的变动性，表现为预测的误差。这就是为什么这里要围绕误差求标准差。当然，这里或许有人会问，那么这里的预测是怎么做出来的？这就又回到第一章的内容：先清洗需求历史，消除促销等不可重复活动的影响，得到基准的需求历史；基于基准的需求历史，选用合适的预测方法，做出基准预测；另行预测未来促销活动等能带来的需求，叠加上去，就得到总的预测；然后计算每期的误差，围绕误差计算标准差和安全库存。

图4：需求呈现明显的趋势、季节性时，如何量化需求的变动性

第二步：量化有货率的要求

接下来我们量化有货率的要求。有货率也叫现货率、库存达成率、服务水平等。简单地说，就是需求来了，库存能够现货马上满足的概率。如果不设安全库存，光靠预测来驱动供应的话，有货率是50%。直观地解释，假定预测是每天100个，供应也是每天100个，一半儿的情况下，实际需求会超过100个，我们没法完全满足；一半儿的情况下，实际需求会低于100个，我们能够完全满足，这就得到50%的有货率。

如果要提高有货率，那就得增加安全库存。如图5示，增加一个标准差的安全库存，有货率提高了34个点，达到84%；再增加一个标准差的安全库存，有货率提高了14个点，达到97%；增加第三个标准差的安全库存，有货率提高了2个点，达到99%多。你马上看出，安全库存的边际效应在递减，为了达到最后几个点的有货率，需要投入很多的安全库存，投入回报太低。所以，对于追求100%的有货率，如果你是销售，可以原谅；但作为供应链职业人，则是不可原谅。

反过来看，如果我们想达到特定的有货率（服务水平），需要放多少个标准差的安全库存？我们可以反算出来：Excel中有个公式normsinv()（见图5），能帮助我们做这样的换算。这就是在量化有货率的要求。简单地说，有货率对应相应的有货率系数，两者之间是1对1的关系，有货率要求越高，这个倍数越大；反之亦然。在数理统计中，这就是在计算正态分布的Z值，也可以通过查正态分布的表格得到。

直观地说，有货率可以折算成一个系数（Z值）。有货率越高，这个系数越大，不过两者不是简单的线性关系。

图5：量化有货率的要求

第三步：计算安全库存

在量化了需求的不确定性，量化了有货率的要求后，安全库存的计算其实挺简单：需求的标准差乘以有货率系数，就是安全库存。特别要注意的是，这里的标准差指的是补货周期内的标准差；而我们在图2和图3中计算的标准差呢，一般是以1周或1月为单位。如果两者不一样，我们要做一定的转换，在图6有详细的公式，但要注意在转换的时候，时间的单位要一样，比如需求历史的标准差是按周计算的，那么补货周期也要换算成周。

比如需求历史、预测误差是按周统计，而补货周期是28天的话，该公式就是把每周的标准差转换为每28天（4周）的，后者是前者的√4倍（注意时间的单位要统一，如果用√28就大错特错了）。这也符合常识：补货周期越长，补货周期内的不确定性就越大，需求的标准差也就越大。这个倍数是开根号的关系，而不是一对一的线性关系，从数理统计学的角度可以证明----如果时光倒流到90年代初，我在大学里学习数理统计，还可以现场证明给你看；如今我虽廉颇未老，不过对数理统计的很多细节，却是不能推演了。

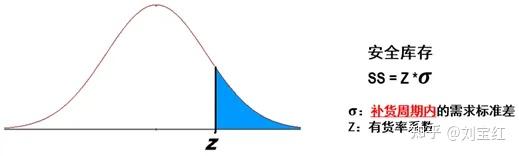
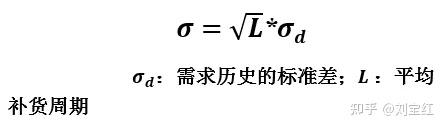
图6：安全库存的计算公式

让我们回到图4中的例子，假定该产品是由供应商加工，采购提前期是3周。假定期望的有货率是95%，我们可以在Excel中计算该产品的安全库存：

计算出来的安全库存是6144个，意味着基于这样的需求历史，和我们预测需求的能力，我们需要设6144个安全库存，才能做到95%的情况下一有需求，我们马上有现货。对这个例子中的供应商来说，我们要给他们提前期内的预测，比如从第8到10周的3周，每周5000个，同时保持6144个的安全库存。所以我们的"毛需求"等于5000*3+6144 = 21144个，减掉在库和在途的库存，得到净需求，就是给供应商的订单。

安全库存的计算本身不难，关键的是我们要计算：通过量化需求的不确定性、量化有货率的要求，基于数据分析，计算出安全库存的数值，然后再根据具体情况，做适当的调整。比如这是个新产品，需求相对旺盛，呆滞风险很低，我们可以考虑多放点；相反，对于生命周期末期的产品，我们可考虑少放点。看得出，安全库存的设置也遵循"从数据开始，由判断结束"的决策方法论。

对很多企业来说，产品动辄几百几千，规格、型号众多，中心仓、前置仓众多，凡是放库存的地方，十有八九都有安全库存。那么多的库存点，没有人知道地比数理统计还多，能把那么多的安全库存设置地更合理。当然，这些公式要求的前提，比如正态分布，我们不一定能完全满足，但这样的计算至少给我们一个相对可靠的起点，让我们来调整。不然，我们就只能完全靠判断、拍脑袋了。要知道，数理统计就是基于大数据，更加科学地取代我们拍脑袋。

对于很多读者来说，平日可能是按照经验值来设定安全库存，比如A类物料放两周，C类放3周的安全库存等。这不科学，但我想补充的是，这种做法也是整合了很多历史经验，包括你们所吃过的苦、受过的罪----比如太多导致的过剩，太少导致的短缺。所以，对于这些经验值，也不要一棍子打死。一方面，有些产品不符合上述公式对正态分布的假设，在我们找到更合适的公式之前，还得靠老经验来计划；另一方面，这些经验值也可以帮我们初步判断，我们按照公式计算出来的安全库存是否大错特错。

对很多人来说，刚开始用这些公式，会经常有这样那样的问题，比如公式套错，数据整理有问题，公式的基本假定没满足，导致计算的结果跟经验值会大相径庭。这很有可能是我们算错了的信号，要特别重视。毕竟，你作为一个企业，多年这么做下来，现在做的是有原因的，也是有一定的合理性；如果新的方法让老的方法看上去非常不合理，那八成是新的方法有问题。

看上去对不对？这是另一种形式的"从数据开始，由判断结束"。尊重自己的直觉。如果你觉得错了，那八成是错了。