需求预测：季节性带趋势的预测

需求的延续性有三种基本形式：其一，随机变动，也就是说忽高忽低，但没有趋势和周期性；其二，趋势，也就是说随着时间发展，需求呈现增长或者降低的趋势；其三，周期性，也就是说需求呈现交替性的高峰、低谷，季节性就是其中一种。再就是趋势和周期性的组合。

对于有趋势的季节性需求，本文介绍一种常用的预测方法，准确度不如霍尔特-温特模型那么高，但相对简单易行，每个人在Excel表格中即可实现。在介绍具体模型前，我们先看一下季节性和周期性的区别。

周期性是时间序列呈现出波浪形起伏，上下起伏，一般由商业和经济活动引起。它不同于趋势，不是朝着单一方向的持续运动，而是涨落相间的交替波动；它也不同于季节变动，季节变动有固定的规律，而循环波动则无固定规律（百度百科，"周期性"词条）。可以说，周期性和季节性都有波峰波谷，前者缺乏规律性，可预见性低；后者规律性强，容易预见。

提到季节性，人们想到的就是一年四季。这没错，不过季节性不一定非得要一年：一天、一周、一个月，甚至一个小时，一分钟，都可以有季节性。

比如你开个餐馆，早饭、午饭和晚饭的需求量不同，对人工的需要早晨少，中午和晚上多，这是一天的季节性。同样，作为餐馆，周五、周六的晚上生意一般最忙，而周二的晚上一般最闲（这也是在美国，很多餐馆周二有特价的原因），这是一周的季节性。

电商也类似，不过跟餐馆的周期性正好相反：周末的时候，小姑娘们都出去逛街吃饭，没多少人在网购；周二的时候，更多人窝在家里不出去，你会发现网购的量会更高----至少这是美国的情形，我在分析一个跨境电商的业务时，看到类似的模式。

如果是单纯的季节性，季度与季度之间没有趋势的话，我们可以求出每个季节跟平均值的比值，用来预测下一年各季的需求。就如下面的例子中，上年四个季度的平均值已知（2500个），根据每个季度的实际需求，就可求出每个季度对应的季度系数。

季度 实际需求 季节性系数

春季 2000 2000/2500 = 0.8

夏季 3500 3500/2500 = 1.4

秋季 3000 3000/2500 = 1.2

冬季 1500 1500/2500 = 0.6

假定下一年这个产品的需求增长30%，那么总预测就是13000，每个季度的平均预测是13000/4=3250，相应地可以预测每个季度的需求。注意，因为需求的聚合效应，预测一年要比分别预测四个季度或12个月的更准确。所以，企业一般会基于一定的假设，预测下年的全年需求，然后参考季节性分解到每个季度或每个月。

季度 预测

春季 3250 * 0.8 = 2600

夏季 3250 * 1.4 = 4550

秋季 3250 * 1.2 = 3900

冬季 3250 * 0.6 = 1950

这其实也不难。有趣的是，读英特尔前CEO格鲁夫的书，其中提到，照相机用的胶卷就是这样的季节性产品，即便在每年的需求量变化不大的情况下，在匈牙利的计划经济时代，那些国营企业还是没法生产出合适的量来（格鲁夫是匈牙利裔）。计划经济之"计划"性，可见一斑。

我们下面看一下季节性、趋势并存的情况（这部分参考了Ron Lembke博士的文章Forecasting with Seasonality）。如图 1，假定这个产品的销量具有季节性，每四期是一个周期；同时，需求也呈现出趋势。我们的任务是预测第13到16期的需求。这里的"期"可以理解为季、月、周、天等任何时间单元（案例中的期其实是季度）。

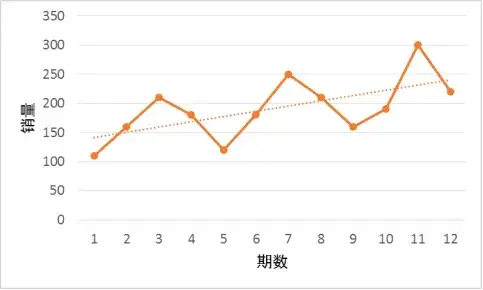
图 1：季节性和趋势并存的时间序列

我们先求每一期的季节指数。如表 1，鉴于季节性每4期循环一次，我们把12期的数据分为三轮（可以理解为3年），求出每期的三轮平均值。每期的平均值与12期的总平均值相比，就得到该期的季节指数。比如第二期的平均值为176.7，12期的总平均为190.8，两者相除，得到第二期的季节指数为0.93，意味着第二期是平均需求的93%（低于100%的话，可以理解为淡季；高于100%，可以理解为旺季）。

表 1：季节指数的计算

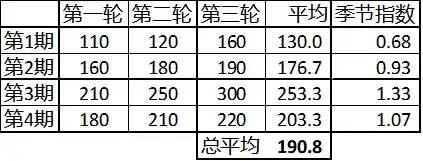
接着我们求趋势。在求趋势前，我们先得去季节化，也就是每期的需求除以季节指数。如表 2，第④列就是假定没有季节性时，每期的需求。围绕第①和第④列的数据，我们来运行线性回归（线性回归在我的《需求预测和库存计划：一个实践者的角度》一书里有详细介绍），得出线性回归方程为需求预测=152.44+5.91*期数。这里的5.91就是我们说的"趋势"，也就是，每期比上期增加5.91个。这样，我们就能够求出不包含季节性的线性预测，见第⑤列。比如第13期的线性预测等于152.44+5.91*13=229.27，四舍五入为229。

最后一步呢，就是把季节指数反算进去，求得季节性调整后的预测，亦即我们最终需要的预测。这是拿线性预测（第⑤列）跟季节指数（第②列）相乘。比如第14期的最终预测就是235*0.93=218。

表 2：预测趋势和季节性并存的情况

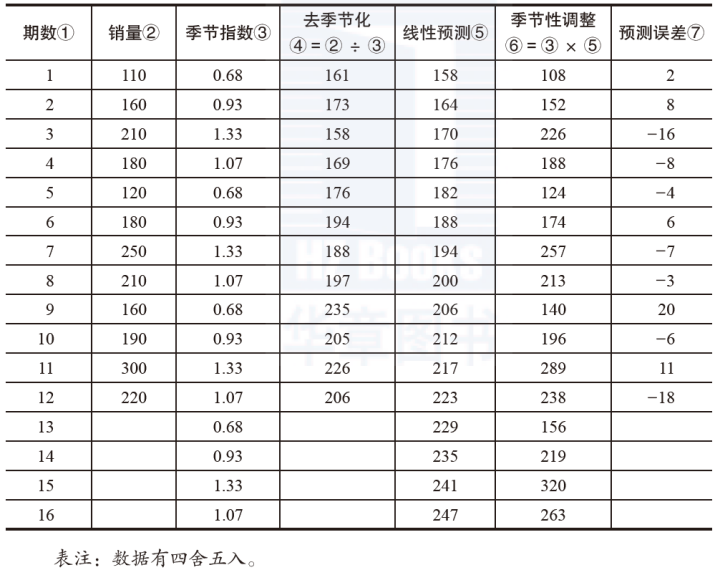
看到这里，有些人或许或问，现在的产品生命周期都这么短，哪能有两年、三年、四年的需求历史，让我们来求这些季节指数、趋势，预测未来的需求？从具体的成品来说，这或许没错；但对半成品、原材料、产能来说，却未必。

比如你是卖热饮的，季节性非常明显的产品，热饮的包装就如快时尚，更新频次相当高；但热饮本身（半成品）和原材料的变化却没那么大，生产线和工艺也是年复一年差不多，我们在半成品、原材料、产能层面还是可以做类似的预测，指导整个供应链更加有序地响应。

我们再回到图 1的例子。这是个完美的季节性带趋势的例子，我们可以相当准确地预测出来（从第⑦列的预测误差即可看出）。实践中，我们很少会有这样的完美情况。我们的应对方案还是尽量作准，尽快纠偏：

尽量作准是寻找更合适的预测方法，通过优化各参数，来尽量提高预测准确度；尽快纠偏是有了一点实际销售数据，要尽早分析，与原来的预测比较，与历史数据比较，再结合市场、销售、产品管理等的职业判断，尽快调整预测。这样做，至少可以避免大错特错。

此外，不管是季节性，周期性，还是趋势，都是相对特定的供应链响应周期、响应能力而言。

当供应链的响应周期很短，响应能力无限的时候，对这些变动性的预测就不那么重要。比如这是个前置仓，或者门店，补货周期就那么几个小时或几天，反映不出来多少季节性、趋势，你也就用不着采取复杂的模型来预测----移动平均法，简单指数平滑法，甚至卖一补一的"幼稚预测"，八成就能够很好应对。

但是，如果你要规划前置仓、门店的规模，决定是否扩容的话，那可是长周期行为，我们得预测未来几个季度甚至几年的需求，这时候，季节性、趋势等更复杂的情形预测就更必要。产线的产能、供应商的产能、长周期物料的备料也是同理。